Shivam Vats

I am a final year robotics PhD candidate at CMU co-advised by Prof. Maxim Likhachev and Prof. Oliver Kroemer. My research is focused on leveraging planning for efficiency in robot learning. In my work, I have come up with algorithms that tell a robot what to learn so that it makes the best use of the available resources. This is important in human-robot collaboration and contact-rich manipulation tasks where acquiring data involves bothering a human or querying a slow simulator. I am currently looking at ways to use planners for guidance in hard reinforcement learning tasks.
More broadly, I am excited by problems that involve both planning and learning, for example, planning with learned models and using learning to speed up planning.
I am grateful for coverage of my work by ASME, CMU News and ACM among other news platforms.
Note: I am actively searching for full-time research and postdoc positions in robotics. Feel free to reach out at svats[at]cs.cmu.edu.
Before joining CMU, I studied maths and computing at Indian Institute of Technology (IIT) Kharagpur where I worked with Prof. P.P. Chakrabarti and Prof. Bibhas Adhikari on heuristic search and simplicial complexes. I was a core developer of SymPy and an active contributor to SymEngine for many years. I also regularly participated in the Intelligent Ground Vehicle Competition as a member of the Autonomous Ground Vehicle Group.
news
| Feb 23, 2024 | Invited talk on Planning What to Learn at the Georgia Tech RoboGrads Seminar (slides). |
|---|---|
| Nov 5, 2023 | Presented SCALE at CoRL, 2023 in Atlanta. |
| Nov 4, 2022 | Invited talk at Prof. George Konidaris’ group at Brown. |
| Nov 1, 2022 | Invited talk at Prof. Lerrel Pinto’s group at NYU. |
| May 27, 2022 | I was a finalist for the outstanding HRI paper award in ICRA. |
selected publications
-
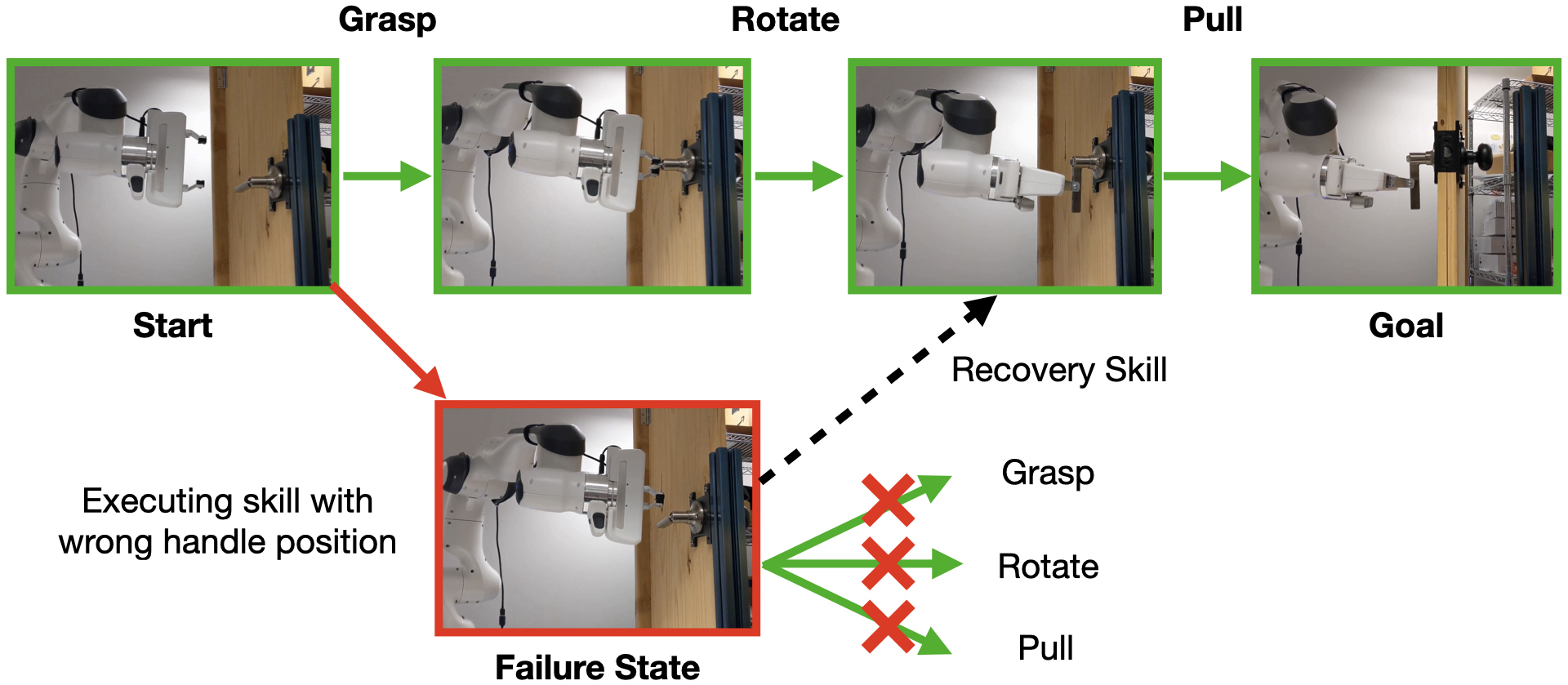 Efficient Recovery Learning using Model Predictive Meta-ReasoningIn 2023 IEEE International Conference on Robotics and Automation (ICRA), 2023
Efficient Recovery Learning using Model Predictive Meta-ReasoningIn 2023 IEEE International Conference on Robotics and Automation (ICRA), 2023 -
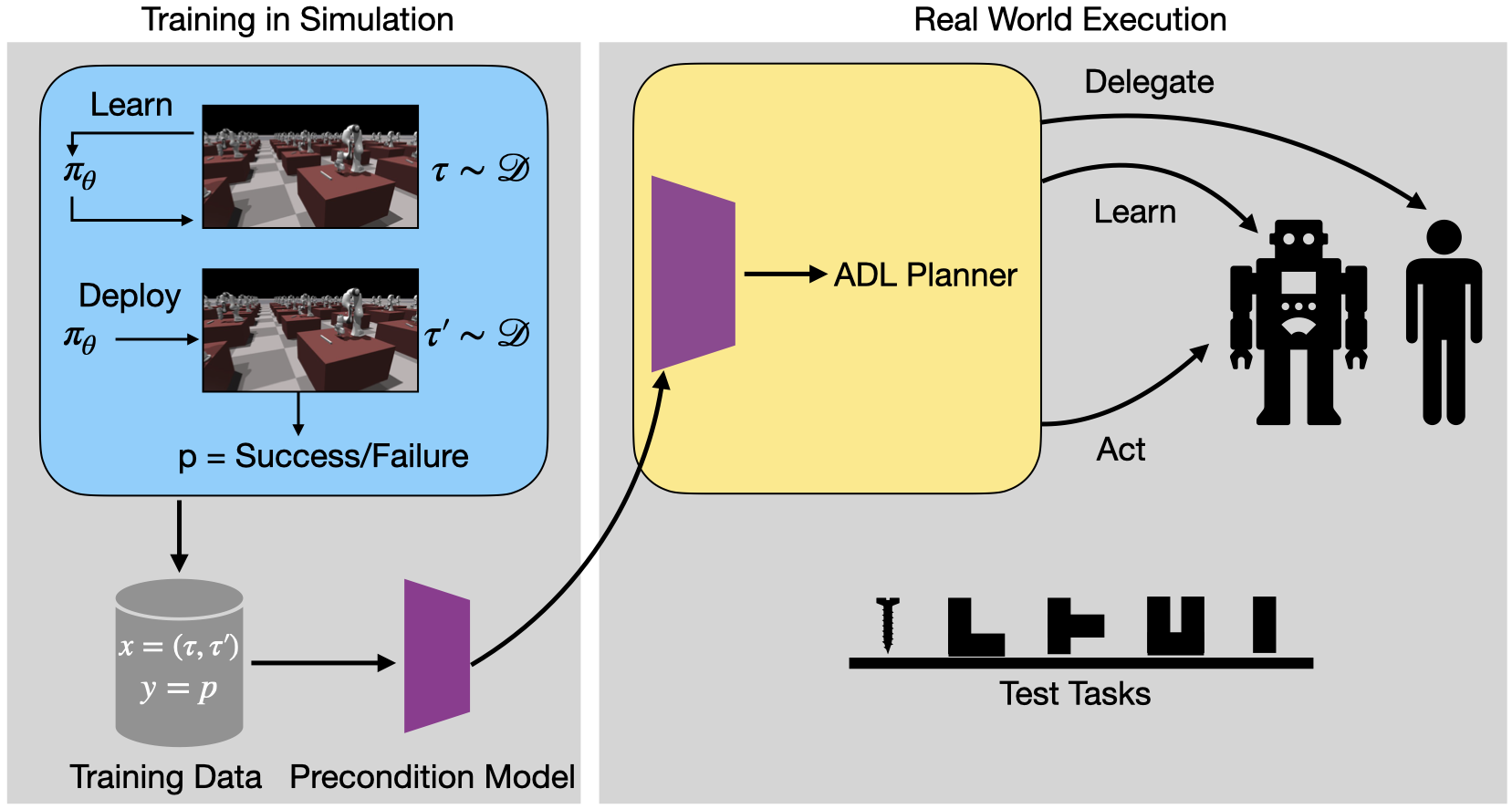 Synergistic scheduling of learning and allocation of tasks in human-robot teamsIn 2022 International Conference on Robotics and Automation (ICRA), 2022Finalist for the Outstanding Paper Award in Human-Robot Interaction
Synergistic scheduling of learning and allocation of tasks in human-robot teamsIn 2022 International Conference on Robotics and Automation (ICRA), 2022Finalist for the Outstanding Paper Award in Human-Robot Interaction -
